Homework Challenge: Trees
**Q: **
Decision trees are piecewise constant models that use data to determine the number of location of cut points.
But can we do the same for piecewise linear or higher order polynomial models as well?
Challenge: design and implement a piecewise linear or higher order polynomial decision tree. Feel free to use simulated data to demonstrate the effectiveness of your method.
A:
如果我们考虑每个属性为坐标空间的每一个坐标轴,则样本的d个属性对应了坐标轴的d个维度,对样本分类意味着在空间中寻找不同类样本的分类边界。而决策树的分类边界有明显的特点:轴平行,即它的分类边界由若干个与坐标轴平行的分段组成,因而也被认为是 piecewise constant models。
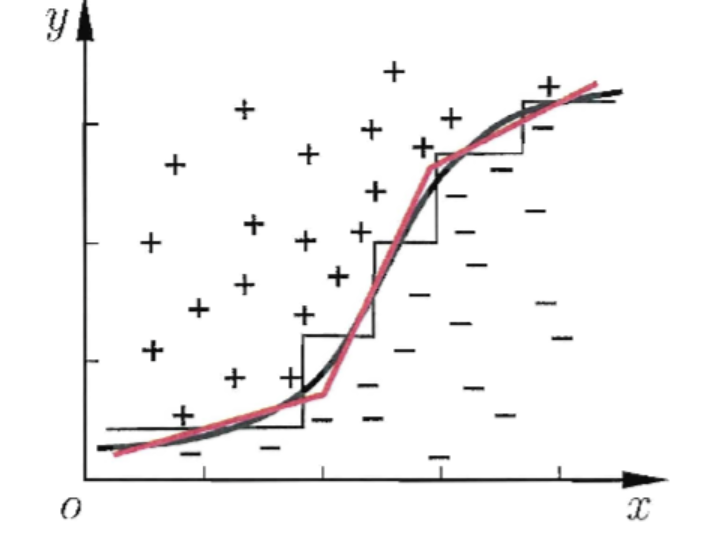
但在学习任务的真实分类边界比较复杂时,必须使用很多段划分才能获得较好的近似。多变量决策树使用斜的划分边界,在此类决策树中,非叶结点不再是仅对某个属性,而是对属性的线性组合进行测试。
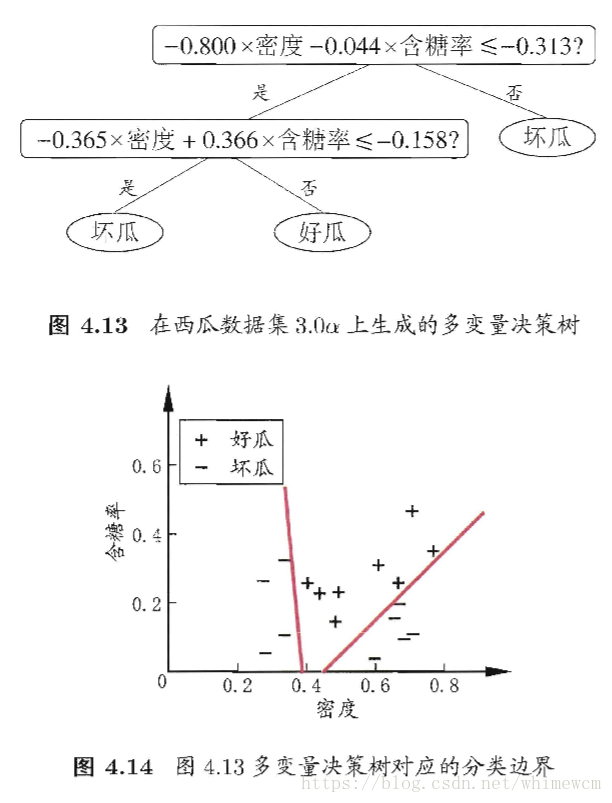
以周志华的《机器学习》书中的西瓜数据集为例,密度和含糖率作为特征,拟合的多变量决策树结果为:
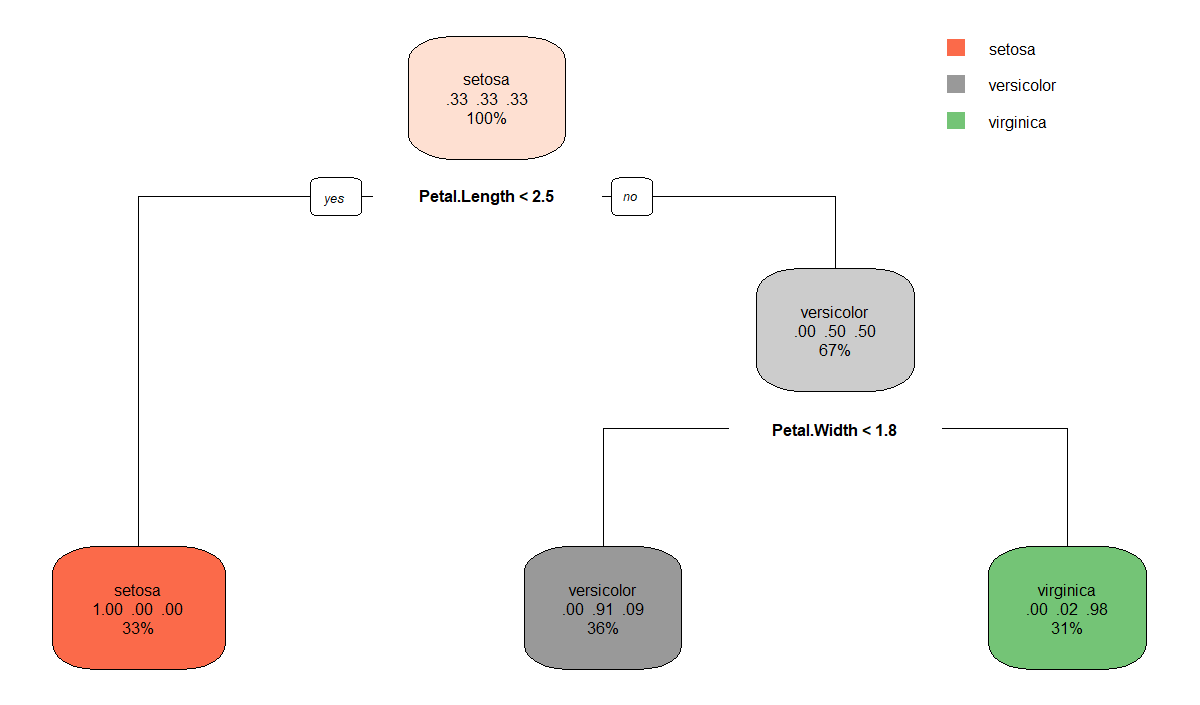
我们以鸢尾花数据集为例,比较单变量决策树和多变量决策树的拟合效果。我们以种类为响应变量,花瓣宽度和花瓣长度为特征,拟合决策树,得到决策树结果如下:
我们可以将此决策边界与散点图一同画出来:
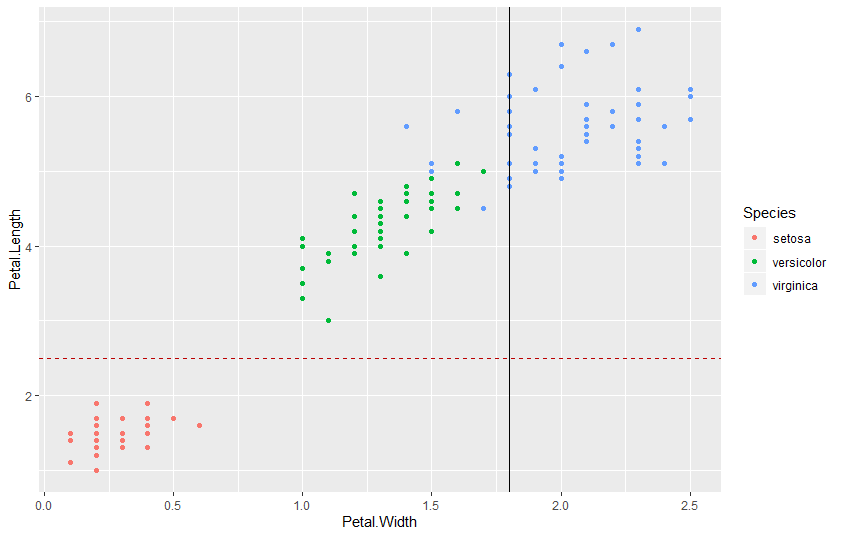
可以看到第二个区分 “versicolor” 和 “virginica” 的决策边界并不理想,存在一些误分的样本。
若我们采用多变量决策树的方法,同样将决策边界与散点图画出来:
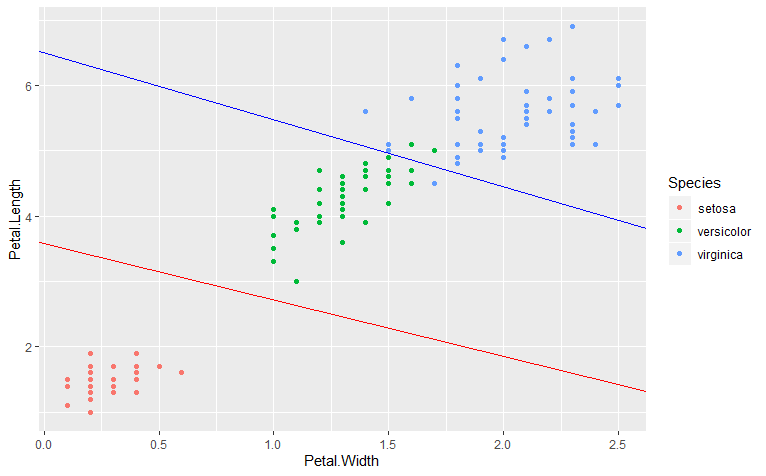
可以看到,在区分 “setosa” 的效果上,两种分类边界没有太大差异,但是区分 “versicolor” 和 “virginica” 的决策边界,分段线性要比分段常数的效果更好。
依此类推,我们可以将多变量决策树扩展到更高阶的情形下。但在处理一些更加复杂的数据时,多变量决策树真的会比CART树表现的更好吗?决策树本身就存在一定的过拟合问题,多变量决策树的过拟合也会是一个问题。
